Our website is being redesigned. This is a temporary page. The next meeting of BAMA will be an online Zoom meeting on Tuesday October 1, 2024.
Instructions for how to join the Zoom meeting and a description of the meeting:
Hannah Kerner Larson Moduli Spaces
Via Zoom at 7:30 pm October 1, 2024
https://scu.zoom.us/j/92100692247?pwd=ANNMIKCbN5srzfbZM1EGpthVcUvxaQ.1
Please join meeting between 7:15 and 7:30 pm
Meeting ID: 999 1775 5772 Password: 617864
One tap mobile: +16699006833,,92100692247#
Join by phone: +1 (669) 900-6833 Meeting ID: 921 0069 2247
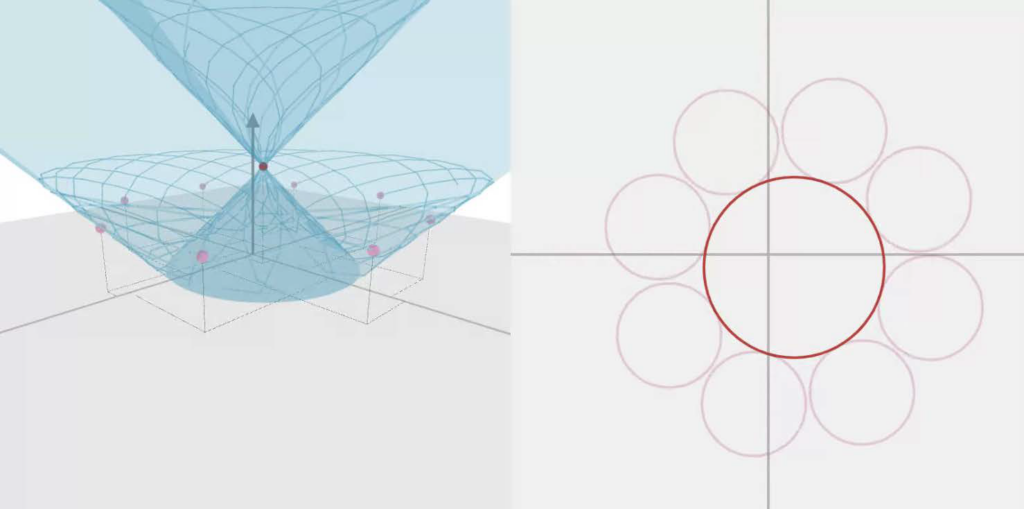
A moduli space is a space where each point corresponds to a shape of some kind. It helps us study all shapes of a given kind together. In this talk, we’ll take a guided tour of the moduli space of triangles and the moduli space of circles. I hope the concept of moduli will give you a new perspective of these familiar shapes!
Hannah Kerner Larson is an Assistant Professor of Mathematics at UC Berkeley and a Clay Research Fellow. She received her Ph.D. from Stanford, where she was advised by Ravi Vakil. Her research centers around moduli spaces and algebraic curves.